При каком положении ручки ворота
Ведро с водой свисает с ворота колодца, тяжелая ручка ворота находится в нижнем положении (рис. 1). Если ведро отпустить, оно начнет двигаться и достигнет дна колодца.
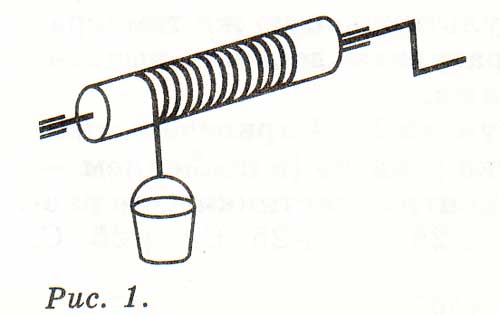
Подберем количество воды таким, чтобы, при его уменьшении ведро при движении не достигало дна. При каком положении ручки ворота система в этом случае может находиться в равновесии? Веревку считайте легкой. Трением можно пренебречь.
Введем обозначения: масса ведра с нужным количеством воды М, радиус ворота R, масса ручки ворота, представляющей собой груз на конце рычага, m, длина рычага l. Обозначим через а угол рычага с вертикалью, при котором система находится в равновесии, и запишем условие равновесия:
МgR=mglsin а. (1)
Положений равновесия два — при верхнем и нижнем расположениях ручки ворота (рис. 2).
Условие задачи — масса воды минимальна, а ведро еще достигает дна — можно выполнить в случае, если ручка «доедет» до верхнего положения равновесия, имея при этом почти нулевую скорость (в пределе — точно нулевую).
Теперь воспользуемся законом сохранения энергии. Ведро опустилось из начального положения на
дельтаh1=R(пи – а) (а — в радианах).
Ручка ворота поднялась из нижнего положения на дельтаh2=l + lсоs а=1(1+соs а).
Начальная и конечная кинетические энергии системы равны нулю. Тогда, в соответствии с законом сохранения энергии, можно записать
Mgдельтаh1 = mgдельтаh2, или МR(пи — а) = ml(1 — соs а). (2)
Из соотношений (1) и (2) получаем
пи-а= ctg(a/2), или a+ctg(a/2) = пи
Это уравнение легко решить численными методами или даже простым подбором по таблице.
Окончательный ответ: а = О,81 рад = 46°.
автор Б. Корсунский