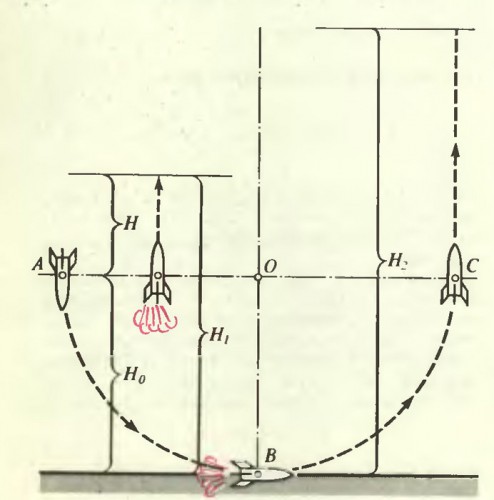
Представим себе, что у нас есть одноступенчатая ракета, имеющая наибольшую высоту подъема Н в поле тяготения планеты, и самолет или аэростат достаточной грузоподъемности, способный поднять указанную ракету на высоту Н0. Какой наибольшей высоты позволяет достичь подобная система? Обычно ответ на этот вопрос следует практически мгновенно: «В соответствии с законом сохранения энергии, наибольшая высота Н1=Н+Но» — и является ошибочным. В чем же дело? Рассмотрим математический маятник с нитью длиной Но, точка подвеса которого О находится на высоте Но над поверхностью планеты (см. рисунок). К свободному концу нити прикрепим нашу ракету, отведем ее в крайнее левое положение (в точку А) и отпустим свободно падать. Пусть в тот момент, когда ракета проходит самую нижнюю точку (точку В) траектории (считаем, что ракета движется «носом вперед»), включается ее двигатель, а когда ракета достигает крайнего правого положения (точка С), она освобождается от крепления, к нити и движется далее свободно. Рассчитаем, на какую высоту Н2 она поднимется.

Подробнее…

Можно добавить горячую воду так, чтобы она равномерно смешивалась с холодной. Для этого воспользуйся душем, только его надо поставить под правильным углом. Коль уж речь пошла о душе, сделай простой опыт. Погрузи душ в воду, направляя его слегка кверху. Струи воды, бьющие из душа, останутся под водой, но если душ поднять еще больше кверху, струи начнут бить гораздо выше, заливая стены и потолок ванной комнаты.

Почему в воде струи из душа движутся гораздо медленнее, чем в воздухе?

Почему при добавлении горячей воды температура в ванне повышается прежде всего у поверхности?

Волшебная картошка

Самые простые и известные вещества коричневый раствор йодной настойки из аптечки и сухой белый порошок — крахмал, который используют для приготовления киселя. Если их соединить, происходят интересные дела: вместо белого порошка и коричневой жидкости получится смесь синего цвета. Химики говорят, что «йод является реакти­вом на присутствие крахмала», а «крахмал служит индикатором (указа­телем) присутствия йода».

Крахмал в том или ином количестве имеется в большинстве продук­тов, которые мы едим. Давайте вооружимся пипеткой и пузырьком с йодной настойкой и определим, есть ли крахмал в картофеле, хлебе, яблоке, в крупах… Разрежем для этого картофелину и нанесем на срез из пипетки одну каплю йодной настойки (предварительно разбавленной пополам кипяченой подои). Точно так же поступим с яблоком и овощами, которые сможем попросить у мамы, чтобы исследовать. Из хлеба сомнем мякиш, намочим его водой и тоже капнем разбавленной йодной настойки.

Как узнать, где крахмала больше — в картофеле, яблоке, хлебе? Это просто: где синяя окраска ярче, там содержится больше крахмала.

Подробнее…

Несколько важных советов:

1. проводить опыты лучше утром, когда ребенок полон сил и энергии;

2. нам важно не только научить, но и заинтересовать ребенка, вызвать у него желание получать знания и самому делать новые опыты. Например, расскажите ребенку, что на самом деле большинство фокусов великого фокусника Дэвид Копперфильда основано как раз на законах физики;

3. объясните ребенку, что нельзя пробовать на вкус неизвестные вещества, как бы красиво и аппетитно они не выглядели;

4. не просто покажите ребенку интересный опыт, но и объясните доступным ему языком, почему это происходит;

5. не оставляйте без внимания вопросы ребенка – ищите ответы на них в книгах, справочниках, Интернете;

6. там, где нет опасности , предоставляйте ребенку больше самостоятельности;

7. предложите ребенку показать наиболее понравившиеся опыты друзьям;

8. и самое главное: радуйтесь успехам ребенка, хвалите его и поощряйте желание учиться. Только положительные эмоции могут привить любовь к новым знаниям.

Подробнее…

Разводим огонь с помощью шоколада и банки колы.

Подробнее…

Что происходит со смесью крахмала и воды на металлическом листе, расположенном на работающем сабвуфере.

Сочетание “крахмал + вода” является так называемой «не-Ньютоновой жидкостью», т.е. жидкостью, на которую “не действуют” законы Ньютона.

Свойство такой массы – тягучесть. она может вести себя и как жидкость и как порошок.

Другие задачи

Другие опыты и эксперименты

На главную

На простых опытах и экспериментах вы убедитесь, как легко можно обмануть чувства человека.

Другие задачи на нашем сайте.