Вот ещё одна не менее любопытная задача (придуманная Гампсоном, автором «Парадоксов природы»): в поезде, мчащемся, скажем, из Ленинграда в Москву, существуют ли точки, которые по отношению к полотну дороги движутся обратно — от Москвы к Ленинграду?

Оказывается, что в каждый момент в каждом вагоне существуют по крайней мере четыре (или восемь) таких точек. Где же они находятся?
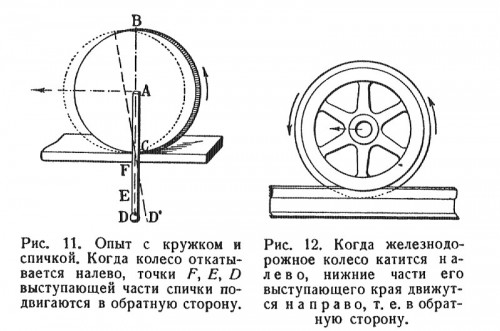
Вы знаете, конечно, что железнодорожные колёса имеют на ободе выступающий край (реборду). И вот оказывается, что самая нижняя точка этого края при движении поезда перемещается вовсе не вперёд, а назад! В этом легко удостовериться, проделав такой опыт. К небольшому кружочку,— например, к монете или пуговице — прилепите воском спичку так, чтобы она прилегала к кружку по радиусу и далеко выступала за край. Если теперь упереть кружок (рис. 11) в край линейки в точке С и начать катить его справа налево, то точки F, Е и D выступающей части отодвинутся не вперёд, а назад. Чем дальше точка края кружка, тем заметнее подастся она назад при его катании (точка D перейдёт в D’).

Точка реборды железнодорожного колеса движется так же, как и выступающая часть спички в нашем опыте (рис. 12).

Вас не должно удивлять теперь, что в быстро мчащемся поезде существуют точки, которые движутся не вперёд, а назад. Правда, это движение длится лишь ничтожную долю секунды; но, как бы то ни было, обратное перемещение в мчащемся поезде всё же существует наперекор нашим обычным представлениям. Сказанное поясняется рисунками 12 и 13.

Автор Я.И. Перельман “Занимательная физика”

Задачи

Общая теория относительности и геометрия

На главную