Ускорение, которое сила тяжести сообщает спутникам, движущимся по орбитам вокруг Земли, зависит от высоты над поверхностью и направлено по радиусу к центру Земли. Результирующая траектория зависит от начальной скорости спутника — как от ее модуля, так и от направления. Один частный случай движения такого типа легко поддается исследованию, а именно, когда спутник движется по окружности. Случай движения по окружности важен и сам по себе, так как многие тела движутся точно по окружности, и как хорошее приближение к действительным орбитам многих спутников. Орбиту Луны в ее движении вокруг Земли, как и орбиту Земли в движении вокруг Солнца, можно в первом приближении рассматривать как круговую.

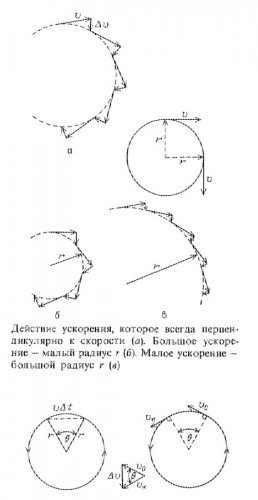
Параболические траектории получаются тогда, когда ускорение постоянно как по модулю, так и по направлению. Круговые траектории получаются тогда, когда ускорение тела постоянно по модулю, но направление ускорения непрерывно изменяется так, что оно всегда перпендикулярно к скорости. На первый взгляд может показаться, что если движущемуся телу непрерывно сообщать ускорение, его траектория постепенно деформируется так, что оно будет двигаться главным образом в направлении сообщаемого ускорения. Именно так и происходит для траекторий в приближении плоской Земли. С другой стороны, если ускорение всегда перпендикулярно к скорости, скорость не может уменьшаться или увеличиваться по модулю. Модуль скорости остается постоянным, но ее направление непрерывно изменяется.

 
Мгновенная скорость тела, движущегося по круговой траектории, направлена по касательной к этой окружности. Вы могли убедиться в этом, когда, выполняя упражнение в «Знакомстве с явлениями», освобождали вращающееся тело. Радиус окружности в каждой точке перпендикулярен к касательной. Поэтому ускорение, направленное по радиусу, всегда будет перпендикулярно к скорости тела, движущегося по данной окружности. Ускорение, необходимое для того, чтобы тело двигалось по определенной окружности, зависит от скорости тела и от радиуса этой окружности. Лишь небольшое радиальное ускорение нужно для удержания медленно движущегося тела на круговой траектории большого радиуса. С другой стороны, потребуется очень большое радиальное ускорение, чтобы свернуть траекторию быстро движущегося тела в маленькую окружность.

Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений”

Интересные научные игрушки