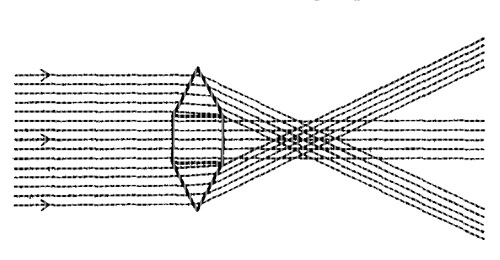
Образование изображений в линзах
Изображения можно получать как с помощью отражения, так и с помощью преломления. С помощью показанных на рисунке призм параллельные лучи сходятся в грубый фокус. Если бы линза была образована бесконечным числом призм, каждая из которых вырезана под должным углом, оказалось бы возможным отклонить каждый из параллельных лучей в одну и ту же точку на оси.
Будет ли такая линза иметь простую форму, сразу не очевидно. Более того, не очевидно, что линза, фокусирующая параллельный свет, будет также создавать изображение объекта, находящегося на конечном расстоянии. Если бы форму линз приходилось рассчитывать заново для каждого положения объекта, линзы вряд ли нашли бы практическое применение. Как мы увидим, существует практическое решение проблемы конструирования линз, как это было и в случае зеркал. Здесь шлифовкой легче всего получить тоже сферическую поверхность. Большинство простых линз имеют сферические поверхности, хотя объективы, используемые в фотоаппаратах или оптических приборах, представляют собой составные линзы, состоящие из большого числа простых линз разной кривизны и с различными оптическими свойствами.
Один из возможных способов расчета линзы состоит в том, чтобы следить за преломлением каждого луча при входе в линзу и при выходе из нее, используя закон Снелла для нахождения пути луча. Еще один способ, действительно лежащий в основе некоторых методов расчета линз, состоит в использовании принципа Ферма. Если свет сходится в фокус после прохождения по разным путям, все участки волны должны прибыть туда в одинаковой фазе, чтобы усилить друг друга в фокусе. Поэтому все пути должны занимать одинаковое время. Посмотрите на приведенный здесь рисунок простой линзы. Поскольку падающие лучи параллельны друг другу, они представляют плоские волновые фронты. Весь свет при входе в линзу имеет одинаковую фазу.
Автор Кл. Э. Суорц “Необыкновенная физика обыкновенных явлений”