Второе уравнение Максвелла выражает закон электромагнитной индукции Фарадея: ЭДС в любом замкнутом контуре равна скорости изменения (т. е. производной по времени) магнитного потока. Но ЭДС равна касательной составляющей вектора напряженности электрического поля Е, помноженной на длину контура. Чтобы перейти к ротору, как и в первом уравнении Максвелла, достаточно разделить ЭДС на площадь контура, а последнюю устремить к нулю, т. е. взять маленький контур, охватывающий рассматриваемую точку пространства (рис. 9,в). Тогда в правой части уравнения будет уже не поток, а магнитная индукция, поскольку поток равен индукции, помноженной на площадь контура.

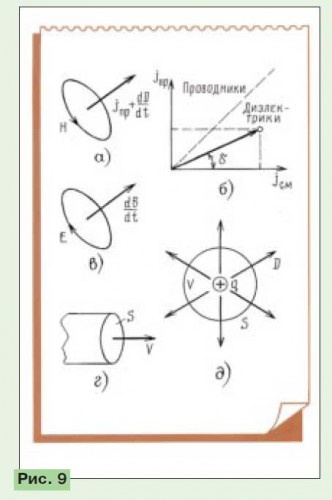
Итак, получаем: rotE=-dB/dt
Таким образом, вихревое электрическое поле порождается изменениями магнитного, что и подано на рис. 9,в и представлено только что приведенной формулой.
Третье и четвертое уравнения Максвелла имеют дело с зарядами и порождаемыми ими полями. Они основаны на теореме Гаусса, утверждающей, что поток вектора электрической индукции через любую замкнутую поверхность равен заряду внутри этой поверхности.

Немного поясним, что такое поток. Если скорость истечения воды из водопроводного крана помножить на площадь отверстия крана. мы получим поток воды — ее расход в кубометрах за секунду (рис. 9,г). Если магнитную индукцию электромагнита помножить на площадь сечения его магнитопровода, получится магнитный поток, определяющий силу притяжения.
В теореме Гаусса для определения потока электрической индукции проще всего взять сферическую поверхность (рис. 9,д) площадью S, во всех точках которой вектор О имеет одинаковое абсолютное значение. По теореме Гаусса SD = q , где q — заряд, помещенный внутри поверхности. Если это точечный заряд, помещенный в центре сферы, то мы получаем простые формулы:

В. Поляков. Журнал “радио” №11-98г.