Поставьте в раковину большой круглый сосуд (кастрюлю или таз), налейте в него столько воды, чтобы ее поверхность образовывала со стенкой сосуда угол около 90°. А теперь приоткройте кран: вода должна капать из крана, не сливаясь в сплошную струю. Ваша задача — не пользуясь какими-либо приспособлениями, попасть каплями воды в самый центр водного зеркала. При этом вы можете либо перемещать сосуд, либо поворачивать вправо и влево кран. А как определить, действительно ли капли попадают точно в середину сосуда или вам это только кажется? Голословных утверждений тут недостаточно, нужны четко выработанные критерии. И, по правде говоря, задача сводится не столько к „прицельной стрельбе” каплями по воде, сколько к умению выработать должные критерии.

При падении каждой капли на поверхности воды образуются поверхностные волны, расходящиеся кругами. Такие же круги расходятся по поверхности любого водоема, если бросить в воду камень. В нашем опыте волны доходят до стенок сосуда, отражаются от них, изменяют направление движения на противоположное и сходятся примерно на середине водной поверхности. Где именно? Это зависит от того, в какой точке они образовались. Понимаете, к чему клонится разговор? Подумайте, как следует, не торопитесь читать дальше.

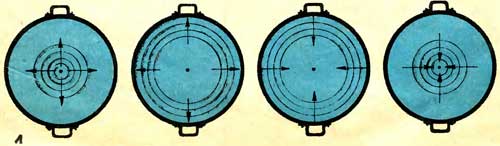
Вам кое-что пришло в голову, не правда ли? Давайте проверим вашу идею, а для этого рассмотрим вопрос в обратном порядке: как будут расходиться волны от капли, упавшей в самый центр водной поверхности? Отсюда разойдутся кругообразные волны; они дойдут до края сосуда (рис. 1), оттолкнутся (отразятся) от него по перпендикуляру и вернутся в исходную точку. Чтобы это заметить, нужно смотреть на поверхность воды под определенным углом; в воде должны четко отражаться предметы, контрастирующие друг с другом или выделяющиеся на окружающем фоне.

А что произойдет, если капля упадет на некотором расстоянии от середины водной поверхности? Тогда волны будут отражаться от краев сосуда под углом не равным 0°. Поэтому, возвращаясь назад, они не пойдут по первоначальному пути и сойдутся в другой точке. В какой? Я думаю, что вы уже во многом и сами разобрались как на основании ваших собственных наблюдений, так и с помощью несложных чертежей, графически представляющих правила отражения волн под углом неравным 0°. Совершенно очевидно, что точка, где собираются отраженные волны, находится тем дальше от середины поверхности, чем дальше от нее упала капля воды. Более того, точка конвергенции отраженных волн симметрична (относительно середины поверхности) точке падения капли воды.

Ну, вот вроде бы и все. Правда, есть еще один вопрос: почему у капель, упавших далеко от середины, точка фокусирования отраженных волн как бы „расплывается”, и чем ближе к краю сосуда, тем более она расплывчата.

Но пора вернуться к нашему опыту. Вы теперь понимаете, почему в том случае, когда волны в сосуде образуются в самом центре водной поверхности, они, отразившись от стенок, возвращаются в ту же самую точку. Ведь они падают перпендикулярно краю сосуда (угол падения равен 0°) и отражаются по той же самой прямой, по которой пришли. Если же волна падает под углом не равным 0°, то она возвращается по пути, отличному от первоначального. Все ли волны должны сойтись в одной точке? Ответить на вопрос поможет простой геометрический чертеж (рис. 3). Начертите окружность определенного радиуса. Нанесите отрезок прямой, проходящей через центр 0 окружности.

На этой прямой обозначьте источник Z на расстоянии d от центра 0. Из точки Z проведите три луча (1, 2, 3). Первый луч проходит через центр О, доходит до окружности в точке Р¹, отражается от нее и возвращается к точке O. Второй идет к некоторой точке Р2 на окружности, отражается от нее и на обратном пути в точке F¹2 пересекается с отраженным от Р1 лучом 1. Третий луч доходит до точки Рз, расположенной точно над центром О и, отразившись, пересекается в точках F13 и F2з с лучами 1, 2, отраженными от Р1 и Р2. Направление последнего луча легко представить на чертеже, так как при своем отражении луч пересекает горизонтальную ось в точке, отстоящей от центра О на расстояние d (лучи отражаются в соответствии с законом отражения, который гласит, что угол падения равняется углу отражения). Чтобы представить луч, отраженный от точки Р2, нужно из этой точки провести какую-либо дугу, пересекающую не только луч 2, но и прямую, перпендикулярную окружности в точке Ра (пунктирная линия на рисунке). Затем следует измерить циркулем расстояние между точками пересечения дуги с лучом 2 и с перпендикуляром и отложить на дуге точку, через которую должен проходить луч 2, отраженный от Р2. А теперь четко обозначим точки взаимного пересечения отраженных лучей. Стало ясно, что в тех случаях, когда источник находится за пределами центра окружности 0, точки взаимного пересечения отдельных отраженных лучей не совпадают, иначе говоря, отраженные волны фокусируются не в одной какой-то точке, а на некотором ограниченном участке. (Каком именно? Это вопрос для наиболее пытливых из вас).

Если бы вместо водяных волн взять световые, а края сосуда заменить сферическим вогнутым зеркалом, то указанную нечеткость в фокусировании отраженных лучей следовало бы назвать сферической аберрацией вогнутого зеркала. В упрощенном виде ее можно представить в виде пучка лучей, одновременно падающих на зеркало (рис. 4). Здесь сферическая аберрация проявляется в следующем: чем дальше от оси зеркала проходит луч, тем ближе к зеркалу пересекает ее после отражения.
Сферическая аберрация не наблюдается у параболических зеркал, которые фокусируют любой пучок, параллельный их оси, в одной точке, независимо от толщины пучка (рис. 5).

Сферическая аберрация свойственна линзам (со сферической поверхностью). Ее можно ослабить, уменьшая диаметр пучка либо применяя более сложные методы. А почему нужно бороться со сферической абер-рацией? Любой уважающий себя фотолюбитель должен знать ответ на этот вопрос.

ЗБИГНЕВ ПЛОХОЦКИЙ
Журнал “Горизонты техники для детей” №4-84г.