Из парафина сделать шарик диаметром 4 см. В шарик вдавить кусочек металла такого размера, чтобы средняя плотность шарика была немного больше, чем у воды. Если такой шарик резко бросить в воду, то он потонет; если же его осторожно опустить на воду, то будет плавать.
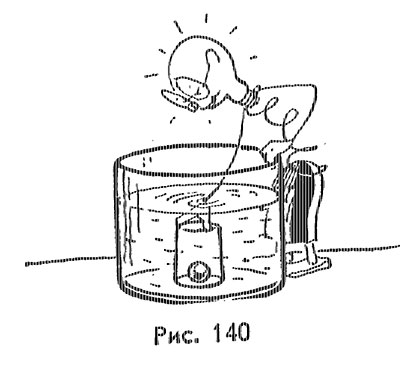
Опустить шарик на дно большого стеклянного сосуда с водой. В этот сосуд погрузить вверх дном стакан (диаметр которого в 2—3 раза больше поперечника шарика) и накрыть им шарик (рис. 140). Поднять стакан вверх — вместе с ним будет подниматься и шарик. Когда шарик будет плавать на поверхности воды, стакан осторожно убрать. Объяснить явление.
Подробнее…
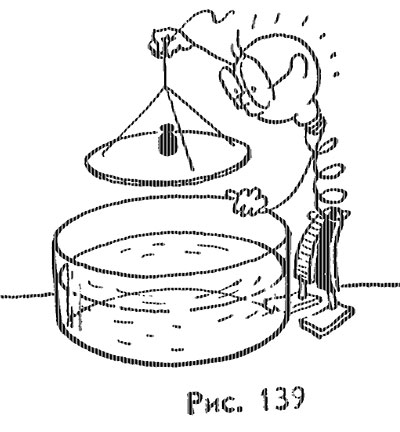
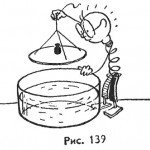
Диск из алюминия (диаметр 20 см, толщина 1 мм), нижняя поверхность которого смазана солидолом, осторожно, держа за привязанные к нему нити, положить плашмя на поверхность воды, налитой в широкий стеклянный сосуд (рис. 139). В центре диска поставить гирю массой 100 г. Почему, несмотря на то что алюминий в 2,5 раза тяжелее воды, диск плавает на ее поверхности?
Подробнее…
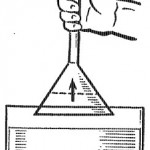
Тщательно промытую стеклянную воронку конусом полностью погрузить в воду, чтобы смочить ее внутреннюю поверхность. Затем вынуть из воды воронку и, закрыв ее трубку мокрым пальцем, погрузить в мыльный раствор. При извлечении воронки из раствора на ее конусе образуется мыльная пленка (рис. 144) отпустите палец. Пленка начнет подниматься вверх пб поверхности конуса внутрь воронки к ее трубке. Объяснить явление.
Подробнее…
«Пляска» камфоры. Чистую кювету наполнить свежей водопроводной водой и поместить на прибор для горизонтальной проекции на потолок. Насыпать мелкие крупинки камфоры на поверхность воды — они начинают энергично вращаться. Капнуть на поверхность воды масла — крупинки камфоры мгновенно останавливаются. Объяснить явление.
Подробнее…
Из тонкого картона (можно взять открытку) вырезать фигуры, изображенные на рисунке 143, и окунуть их в расплавленный парафин.
После застывания парафина фигуры пустить плавать на поверхность воды, налитой в стеклянную ванночку. В расширение прорезей первой фигуры положить небольшие кристаллики камфоры — фигура начнет вращаться по часовой стрелке.

Концом проволоки, смоченной в мыльном растворе, коснуться поверхности воды в точке а второй фигуры. «Ядро» вылетит из «пушки». (Опыты показать в световой проекции на потолок.) Объяснить явление.
Подробнее…
«Склеивание» водяных струй. В консервную банку, в стенке которой пробиты три отверстия диаметром около 1мм каждое (рис. 142), налить воды. Она будет вытекать тремя струйками. Сдавить струи пальцами, проводя ими по стенке банки. Струи соединятся в одну струю. Объяснить явление.

Подробнее…
На столе стоит стакан с водой, узкогорлый флакон (например, от одеколона) и кусок тонкой проволоки. Как Налить воду из стакана во флакон?
Обосновать использованный способ.
Подробнее…
Выскакивающий поплавок (рис. 141). Сквозь большую пробку продеть кусок проволоки толщиной 1—2 мм. К нижнему концу поплавка прикрепить свинцовый груз, а недалеко от верхнего конца проволоки перпендикулярно к ней припаять плоскую металлическую сетку размером 60 х 60 мм.
Вес свинцового груза должен быть таким, чтобы прибор в сосуде плавал стоймя, а верхняя часть пробки немного выступала из воды.
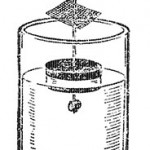
Погрузить прибор так, чтобы сетка оказалась под водой,— он останется в таком же положении. Налить в стакан несколько капель эфира и наклонить стакан над поверхностью воды, в которой плавает поплавок (осторожно, чтобы не вылилось ни капли эфира). Поплавок выскочит из воды, причем сетка окажется над ее поверхностью. Объяснить явление.
Подробнее…
Из парафина сделать шарик диаметром 4 см. В шарик вдавить кусочек металла такого размера, чтобы средняя плотность шарика была немного больше, чем у воды. Если такой шарик резко бросить в воду, то он потонет; если же его осторожно опустить на воду, то будет плавать.

Опустить шарик на дно большого стеклянного сосуда с водой. В этот сосуд погрузить вверх дном стакан (диаметр которого в 2—3 раза больше поперечника шарика) и накрыть им шарик (рис. 140). Поднять стакан вверх — вместе с ним будет подниматься и шарик. Когда шарик будет плавать на поверхности воды, стакан осторожно убрать. Объяснить явление.
Подробнее…
Диск из алюминия (диаметр 20 см, толщина 1 мм), нижняя поверхность которого смазана солидолом, осторожно, держа за привязанные к нему нити, положить плашмя на поверхность воды, налитой в широкий стеклянный сосуд (рис. 139). В центре диска поставить гирю массой 100 г. Почему, несмотря на то что алюминий в 2,5 раза тяжелее воды, диск плавает на ее поверхности?
Подробнее…







